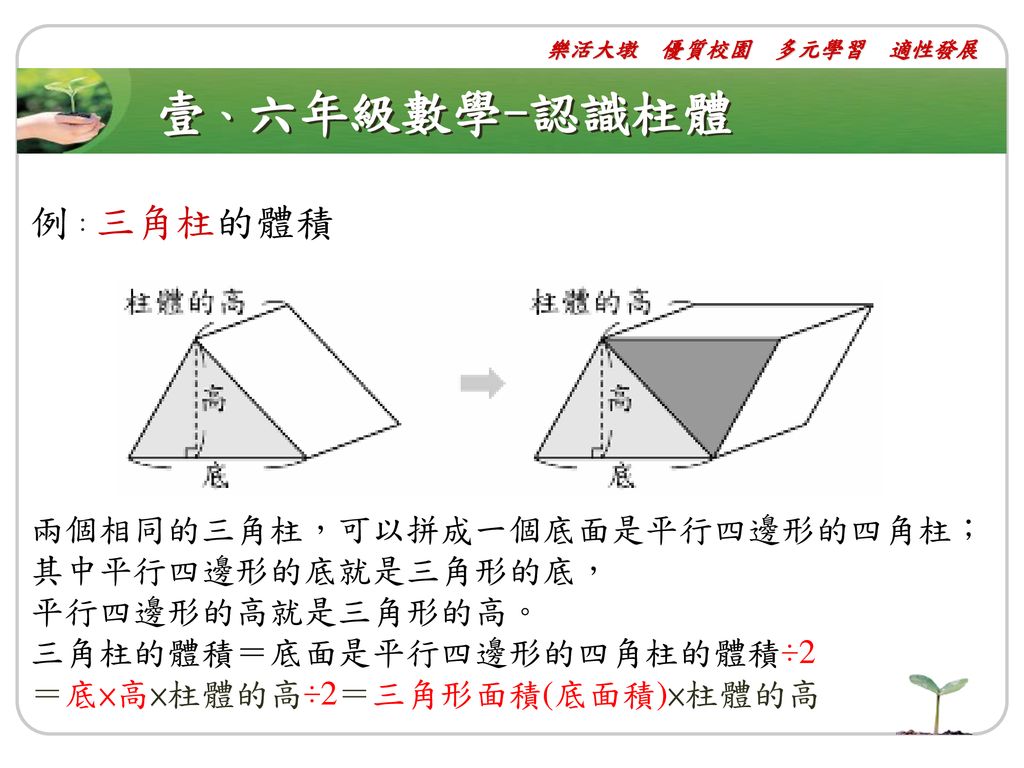
《問題》 底面が一辺a cmの正方形で,高さがh cmの正四角柱がある。この正四角柱の底面の一辺の長さを2倍にし,高さを半分にした正四角柱の体積は,もとの正四角柱の体積の何倍になりますか。《答え》 2倍どうしてこの答えになるのかが次の三角柱の体積を求めよ。 STEP1 底面積を求める まず、底面の三角形の面積 を求めます。 底面は、長さが と の辺が で接する直角三角形なので、底面積 は STEP2 底面積と高さを体積公式に当てはめる あとは、三角柱の体積の公式に当てはめればOK 底面の三角形の面積に、三角柱の高さをかけてください 🔊 Play The volume of a right circular cylinder is the area of a circle times its height 正円柱の体積は、正円の面積に高さをかけたものです 🔊 Play Calculate the product of 6 times the area to find the surface area of the cube
四角柱 维基百科 自由的百科全书
正四角柱 体積
正四角柱 体積-要点四角錐,三角錐,円錐の体積 三角錐,四角錐,円錐の体積 V は,それがちょうど入る四角柱,三角柱,円柱の体積の です. 特に,円錐については,底面の半径が r であるとき,底面積が S=πr 2 と書けるから と書くこともできます.体積 (たいせき) とは、 立体 (りったい) が 空間 (くうかん) の中で 占 (し) める大きさのことです。 このページでは、 様々 (さまざま) な立体の体積の 求 (もと) め方を 一覧 (いちらん) にまとめています。 図形 (ずけい) と体積の 公式 (こうしき) をセットで 覚 (おぼ) えましょう!



2
正四角錐の体積 (底辺と高さ) ツイート 体積・表面積の計算 ・ 立方体の体積・表面積 ・ 立方体の体積から1辺 ・ 立方体の表面積から1辺 ・ 直方体の体積・表面積 下の図4のように切断四角柱(直方体)とわかります。 高さの平均が 体積は、底面積×平均の高さ から求めると 48c㎥ となります。 ( 参考 → 切断された三角柱の体積の求め方 ) 女子学院中学の過去問題集は → こちら 桜蔭中学の過去問題集は → こちら正四角柱の底面の正方形の一辺の長さをa、高さをh 正四角錐の底面の正方形の1辺の長さを2a、高さをh' とすると 正四角柱の体積はa²h 正四角錐の体積は(4a²h')÷3 a²h=4a²h'/3 h'=4/3h
今回は、四角錐(しかくすい)の体積の求め方(公式)について書いていきたいと思います。 四角錐の体積の求め方公式 四角錐の体積を求める問題 問題① 《四角錐の体積の求め方》 問題② 《四角錐の体積の求め方》 問題③ 《四角錐の高さの求め方》 (adsbygoogle = windowadsbygoogle 正四角すいの体積(中学受験算数問題)面の回転と体積(巣鴨中学 受験算数問題09)切り取られた円柱(sapix7月入室、組分けテストより)四角すいの展開図(灘中学 06、ラ・サール中学 1994、同志社女子中学 09、大妻中学 05 類題)直方体と水の入 まとめ:正四角錐の体積の求め方も大丈夫! 正四角錐の体積の公式はどうだった? ? 底面積×高さ×1/3 という計算をゆっくりしてみてね。 テスト前に復習しておくと心強いかも! そん
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題 正四角柱の体積の求め方はなんですか? 数学 締切済 教えて!gooみんなの算数オンライン 中学受験5年Unit42 2 立体図形4 柱の切断 Author みんなの算数オンライン Subject 断頭三角柱、断頭四角柱とは? 断頭三角柱、断頭四角柱は三角柱や四角柱、(円柱も)をひとつの平面でスパッと切ってできる立体です。




角柱の体積 Youtube



四棱柱 搜狗百科
正四角すいの体積(中学受験算数問題)面の回転と体積(巣鴨中学 受験算数問題09)切り取られた円柱(sapix7月入室、組分けテストより)四角すいの展開図(灘中学 06、ラ・サール中学 1994、同志社女子中学 09、大妻中学 05 類題)直方体と 1:高校受験数学の問題で、四角柱の頭部を切断した残り部分の体積を求める公式として 底面積x (abcd)/4(abcdはそれぞれ底面に垂直な辺の長さ) つまり、体積=底面積☓底面に垂直な辺の長さの平均 があるそうですが、なぜそうなるのですか? 同じ立体 数学・算数 某中学校の入試問題です。解答はあるのですが、解説がないため理解できません。 どうか考え方を教えて頂きたく、よろしくお願いいたします。 ≪問題≫ 図のような底面が正方形で、各辺の長(1/2)



大嘴鳥親子雜誌
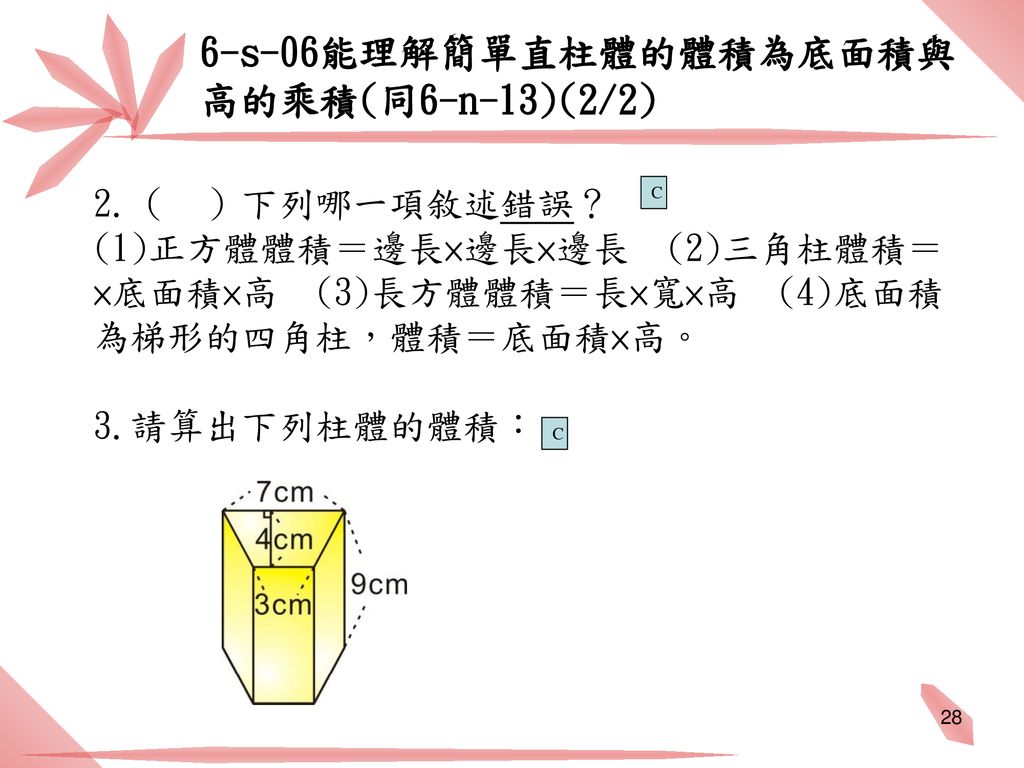



立體圖形 授課篇 適用年級 5 6年級設計者 Mri團隊 Ppt Download
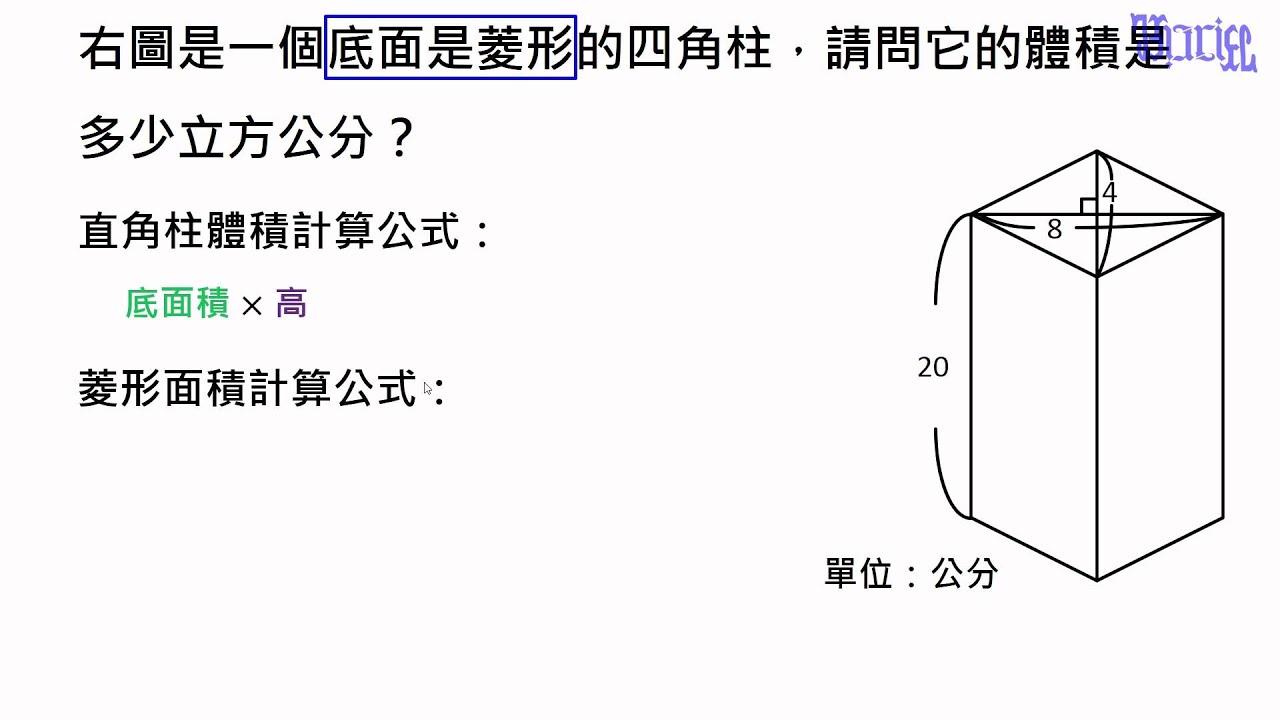
日本大百科全書(ニッポニカ) 角柱の用語解説 平行な2平面α、βとそれらに交わる直線l、およびα上の多角形Pがあるとき、Pの任意の点を通ってlに平行な直線の全体のつくる立体のαとβの間にある部分を角柱(斜角柱)という。このとき、多角形Pを底面、底面でない面を側面という。3 cmのひし形を底面とし,高さが8cmの四角柱がある。 (1) この四角柱の体積を求めなさい。 解 (6×6√ 3 ÷2)×8= 144√ 3 cm 3 (2) 三角錐BFCAの体積は,四角柱の体積の何倍か。正四面体の内接球の半径 この公式の応用例として,1辺が a a a の正四面体の内接球の半径を求めてみます。入試問題で頻出です。 正四面体の表面積と体積は公式として覚えておくとよいでしょう。 →正三角形の面積,正四面体の体積



数学 q 底面の一辺が10cm 高さが5cmの正四角錐の体積は 底面が合 Yahoo 知恵袋




如何做正方體 Simonar
がある。この四角柱の辺のうち,辺ab とねじれの位置にある辺 右の図は,正四角すいと直方体を合わせた形で,点a,b, がある。この正四角錐の体積を求めよ。そして、正四角柱は半分の直角二等辺三角柱にできる。直角二等辺三角柱は3等分すると、同じ底面の錐にできる。だから、錐は柱の体積の3分の1になるのか。 s:円柱も正四角柱にできるんですか? T:こうやって切るとできますよ。 7、球の表面積円柱の体積( V olume) S 底面の面積( S urface area) h 高さ( h eight) π 円周率(= 314) r 底面の円の半径( r adius) 斜円柱の体積の求め方 ここからは、補足的に直円柱と斜円柱について述べ



Mathematics 角錐の体積が角柱の3分の1になる証明 働きアリ
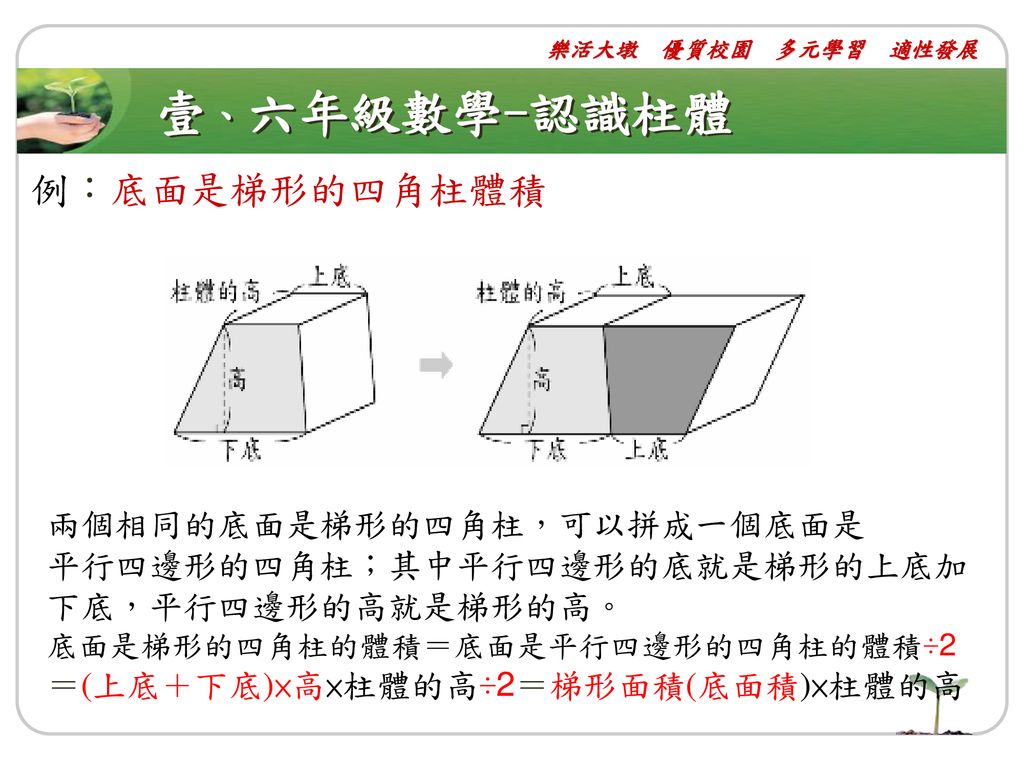



Hd限定四角柱体積公式 最高のカラーリングのアイデア
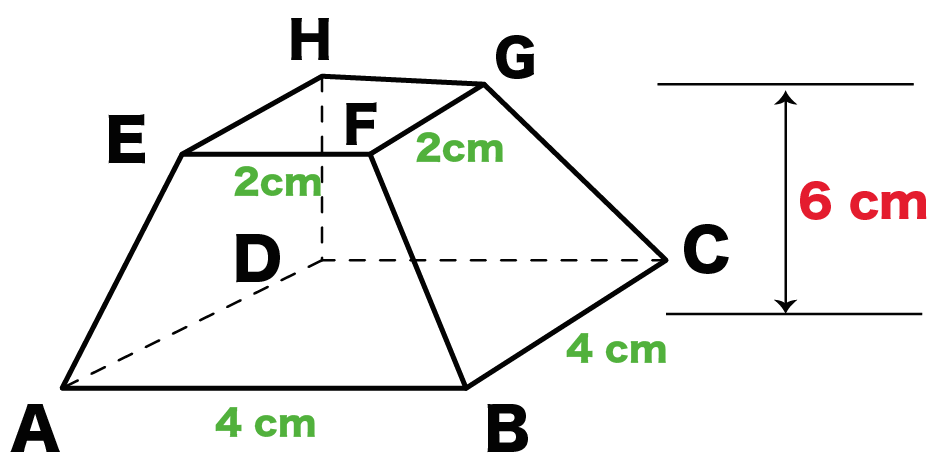
正四角錐台の体積 のことなんじゃないかな。 プリンみたいな立体だよ。 正四角錐台は台形の立体バージョンにみえるし、たぶんそう。。 そこで今日は台形の体積のかわりに、 正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。 は正の数なので =5(cm)となります。 これより側面積=(6×5÷2)×4=15×4=60(cm²) よって、四角錐の表面積=底面積+側面積=36+60=96(cm²)となります。 答え 96cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方1体積を計算する形状を選択します。 2入力項目に入力します。 3計算開始ボタンを押して体積を計算します。 注意 表面積を計算できない形状があります。 楕円の表面積は近似値です。 ご要望がありましたらレビューか電子メールでご連絡ください。



Tankacom Net



大嘴鳥親子雜誌
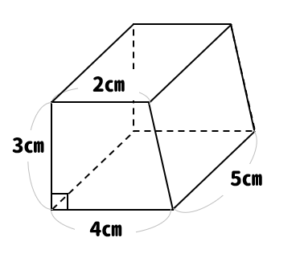
送信を完了しました。 正四角柱の体積 のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 小・中学生 高校・専門・大学生・大学院生 主婦 会社員・公務員 自営業 エンジニア 教師・研究員 その他 この計算式は 非常に役FDE の面積12cm 2, RF=4cm より体積16cm 3 また、四角錐のほうは底面が台形PDEQ である。 高さはRから面ADEBにおろした垂線の長さで、 これは辺FDと同じ長さになる。 台形ADEB の面積(36)×6÷2=27 FD=4cm より体積36cm 3 よって求める立体の体積は1636=52 四角柱の体積=底面積×高さ =(台形の面積)×高さ = {(上底下底)×高さ÷2}×高さ となります。 つまり {(2+4)×2÷2}×3 =18㎤ この問題の答えは18㎤ということになります。 他の四角形の面積についても、これを機に復習してみてはいかが




正四稜柱 上 下底面都是正方形 且側棱垂直於底面的稜柱叫做正四稜柱 正四 百科知識中文網




斜四棱柱表面积 四棱锥表面积计算公式 三人行教育网 Www 3rxing Org
積分を用いた証明 二つ目の説明です。数学2の知識が必要になります。積分を使って V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h を証明します。 底面積の形によらない(円錐でも三角錐でも四角錐でも適用可能)証明方法です。底面積を求めると体積の計算は簡単に済みます。下記も併せて勉強しましょう。 体積の公式は?1分でわかる求め方と覚え方、一覧、三角柱、円柱、三角錐の体積 底面積の求め方は?5分でわかる計算、円柱、円錐、四角柱、三角柱の底面積 管理人お 角柱の体積を求める問題です。 公式自体は難しいのもではないので、図形を見て底面積がどこかをしっかり確認してください。 5年生の角柱の基本事項も復習しておきましょう。 角柱の体積は 底面積×高さ で求めることができます。角柱は底面が三角形なら三角柱、四角形なら四角柱、五




四角柱 Wikiwand




四角柱 维基百科 自由的百科全书
6角柱 六角柱 対辺 体積計算 公式 求め方 高さ 自動 volume用立体模型(高さ1mm):三角柱、正四角錐、四角柱各1個 型番 型式 本体価格 税込価格 C2 ¥ 3 0, 0 ¥ 2, 4 投影図説明器 組立式の投影図台です。 投影板、ベース板はチョークで書き込みでき、マグネットも使えます。



正四角柱の表面積から辺の長さの求め方を教えてください 底面の1辺をa Yahoo 知恵袋



2




Physics Quod Erat Demonstrandum




長方體與正方體有什麼相同點和不同點 Matteffer



如何求金字塔形物體 正四角錐 的體積 中學數學課 隨意窩xuite日誌



数学の問題で分からないところがあります 体積の等しい正四角錐 Yahoo 知恵袋




中学数学 四角柱 Youtube




四棱锥切割体 四棱锥体体积公式 三人行教育网 Www 3rxing Org



3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




正四角錐3つから正四角柱1つがつくれる 中1 空間図形の体積 数楽者のボヤキ ツブヤキ ササヤキ 中学 数学 道徳 Mathematics Puzzles




Hd限定四角柱体積公式 最高のカラーリングのアイデア



長方體




Surface Area Of Prisms And Cylinders Calculations And Formulas Ryosuke University




四角柱 维基百科 自由的百科全书




梯形體積公式梯形體的體積計算公式 百度知道翻譯此網頁 Qbxfp
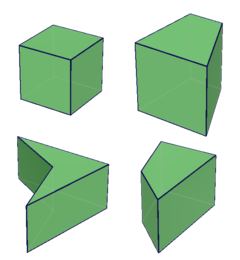



四角柱 维基百科 自由的百科全书




Hd限定四角柱体積公式 最高のカラーリングのアイデア



大嘴鳥親子雜誌



Hd限定四角柱体積公式 最高のカラーリングのアイデア



2




鈄截柱體體積 Quod Erat Demonstrandum




四角柱の体積と表面積の求め方



3




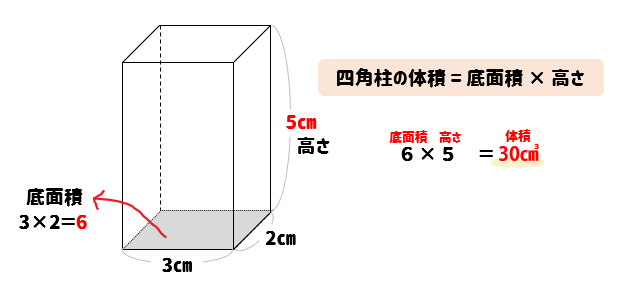
計算公式 四角柱の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



Hd限定四角柱体積公式 最高のカラーリングのアイデア




正四棱锥有关公式 正四棱锥体积公式 三人行教育网 Www 3rxing Org



2




中2の数学で単項式の乗法と除法の範囲です 質問は Clearnote




正四棱锥的表面积 正四棱锥体积和表面积计算公式 谢谢 三人行教育网 Www 3rxing Org




四角柱 Wikiwand




四角錐台の体積 高精度計算サイト




四角柱 维基百科 自由的百科全书




正方體展開圖教具立體圖形 Qaxnl
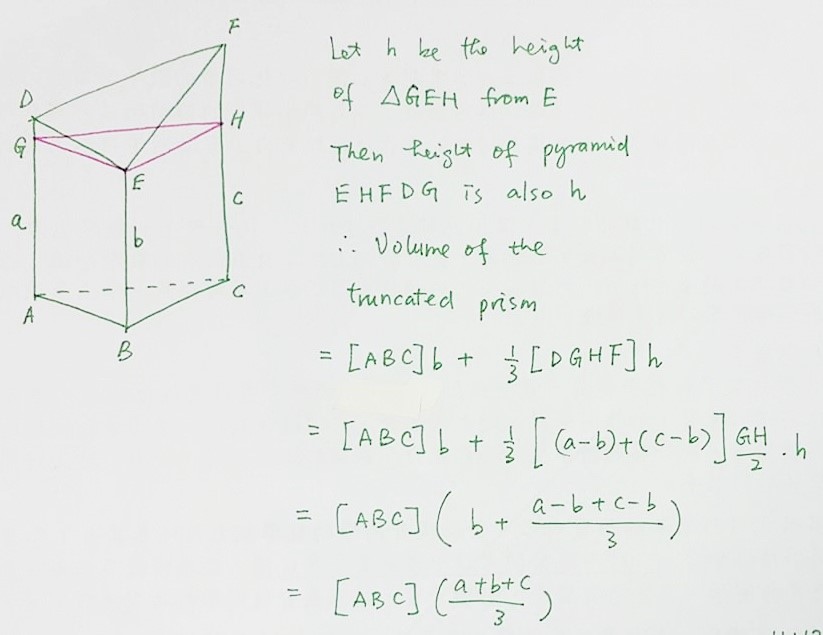



鈄截柱體體積 Quod Erat Demonstrandum




如何做正方體 Simonar



四角柱 维基百科 自由的百科全书
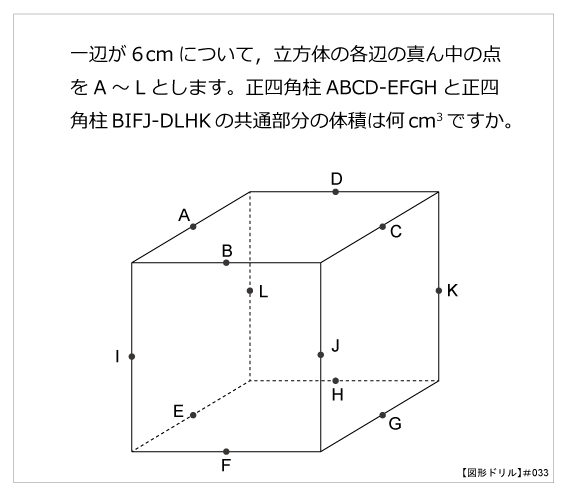



第33問 立方体の共通部分 図形ドリル 第33問 立方体の共通部分 算数星人のweb問題集 中学受験算数の問題に挑戦




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット



数学の問題で体積が600立方センチメートル 高さ10センチメ Yahoo 知恵袋




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題



四棱柱 搜狗百科




Surface Area Of Prisms And Cylinders Calculations And Formulas Ryosuke University




四角柱 维基百科 自由的百科全书



50 素晴らしい角錐体積公式 ページを着色するだけ




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




長方體 Wikiwand




正方體展開圖教具立體圖形 Qaxnl




長方體 维基百科 自由的百科全书




1 Boy的聲音問 Ppt Download



四稜柱 四角柱 概念 性質 特殊的四稜柱 體積與表面積 中文百科全書



1




四角柱 维基百科 自由的百科全书




四角柱 维基百科 自由的百科全书




四角柱 Wikiwand




立體圖形 Geogebra




正四棱锥有关公式 正四棱锥体积公式 三人行教育网 Www 3rxing Org




四棱柱 搜狗百科




四角柱 维基百科 自由的百科全书




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




棱柱的表面积体积公式 求四棱柱的表面积和体积公式 三人行教育网 Www 3rxing Org



Hd限定四角柱体積公式 最高のカラーリングのアイデア



Math 容器にものを入れる問題 公式 体積 底面積 高さ の応用 働きアリ
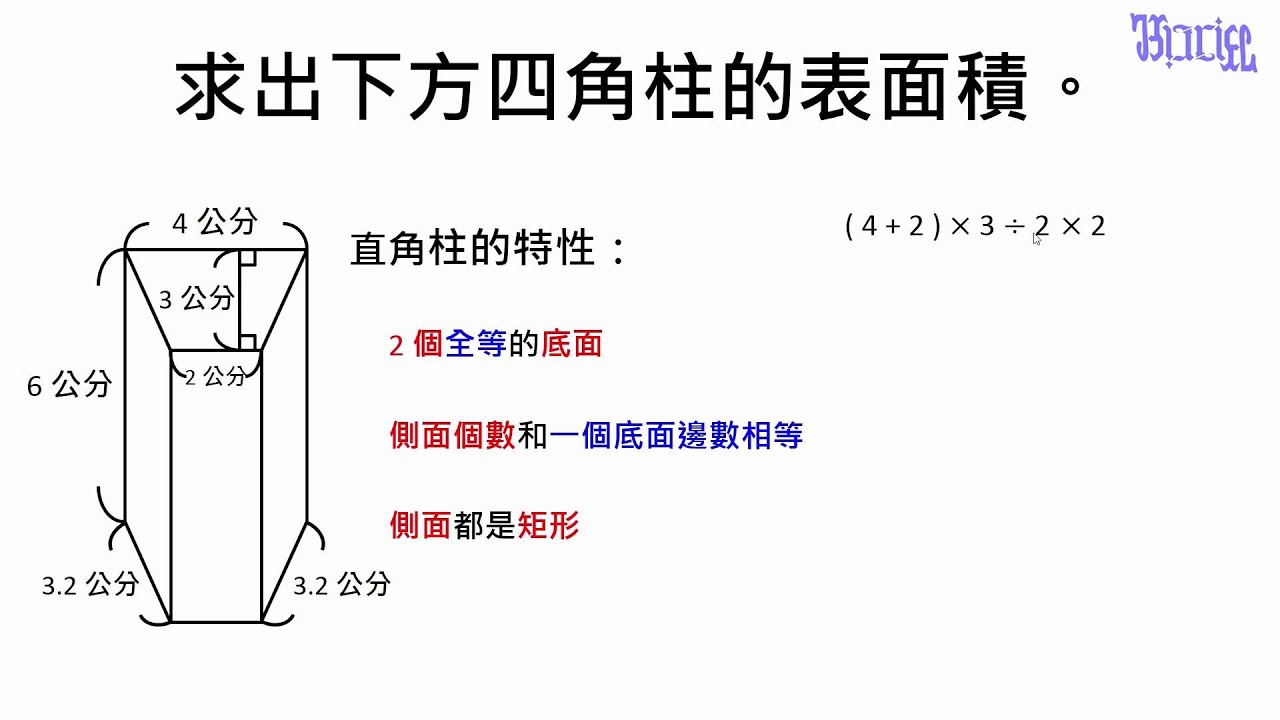



柱體的體積與表面積 04 求出四角柱的表面積 Youtube




Physics Quod Erat Demonstrandum
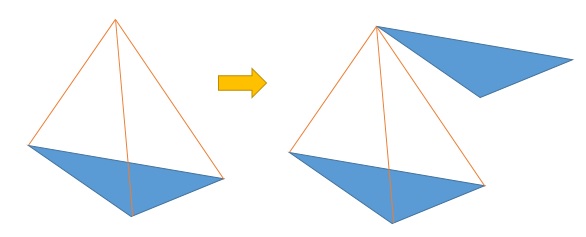



鈄截柱體體積 Quod Erat Demonstrandum



2



式の計算 文字式の利用 図形 清水塾




四角柱 维基百科 自由的百科全书




この問題の解説お願いします 答えは4 3倍です Clearnote



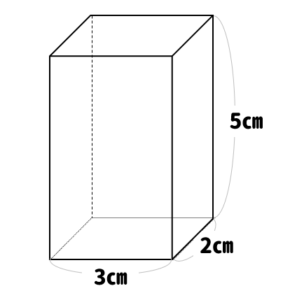
この四角柱の表面積と体積の求め方を教えて下さい 体積は 底面 Yahoo 知恵袋




Physics Quod Erat Demonstrandum




四角柱體立體圖形 四 Uqbfk




この問題の解き方を教えてください お願いします Clearnote




四角柱 维基百科 自由的百科全书



四棱柱 快懂百科
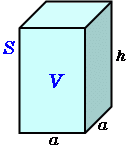



正四角柱の体積 高精度計算サイト




正方體展開圖教具立體圖形 Qaxnl




梯形體積公式梯形體的體積計算公式 百度知道翻譯此網頁 Qbxfp




学調対策テキスト 応用編 数学 図形 3 9 Youtube



正四角柱 正圓柱體



Hd限定四角柱体積公式 最高のカラーリングのアイデア




正四角柱から正四角錐へ Geogebra



最高のコレクション四角柱体積公式 ニーアオートマタ壁紙




斜四棱柱表面积 四棱锥表面积计算公式 三人行教育网 Www 3rxing Org




四角柱 维基百科 自由的百科全书




Hd限定四角柱体積公式 最高のカラーリングのアイデア



この問題で 正四角錐と正四角柱の体積が正しいからと言って 何故 正四角錐 Yahoo 知恵袋




中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット



1




立體圖形 授課篇 適用年級 5 6年級設計者 Mri團隊 Ppt Download



0 件のコメント:
コメントを投稿